최악의 경우 $\Theta(n^2)$의 시간복잡도를 갖지만 $\Omicron(n\log n)$ 평균적으로 가장 좋은 성능을 보이고 구현이 쉬워 현업에서 가장 많이 쓰인다고 알려진 퀵 정렬을 알아보고 자바와 파이썬으로 구현해 봅시다.
퀵 정렬
퀵 정렬(quick sort)은 병합 정렬 알고리즘과 비슷하게 입력을 나누어 각각에 대해 재귀적으로 정렬하는 알고리즘입니다. 퀵 정렬과 병합 정렬의 차이점은 크게 두 가지가 있습니다. 퀵 정렬은 병합 정렬과 달리 합치는 과정이 없고 입력을 항상 반씩 균등하게 나누지 않습니다. 퀵 정렬은 기준값정하고 기준값보다 큰 값들과 작은 값들로 입력을 분할합니다. 이때 기준값을 피벗(pivot)이라 합니다.
- Pseudocode
quickSort(A[], first, last){
if( first < last ){
p ← partition(A, first, last); // 피벗의 위치
quickSort(A, first, p-1);
quickSort(A, p+1, last);
}
}
partition(A[], first, last){
배열 A[first ⋯ last]의 원소들을 피벗을 기준으로 재배치하고
재배치된 피벗의 위치를 반환한다.;
}partition 함수를 조금 더 자세히 표 헌 하면 아래와 같습니다.
quickSort(A[], first, last){
if( first < last ){
p ← partition(A, first, last); // 피벗의 위치
quickSort(A, first, p-1);
quickSort(A, p+1, last);
}
}
partition(A[], first, last){
pivot ← A[last]; // 마지막 원소(A[last)를 피벗으로 사용
i ← first-1; // 피벗 왼쪽 부분의 마지막 위치 (피벗보다 작은 부분)
for( j ← first to last-1 ) // 피벗과 비교할 요소의 커서
if( A[j] < pivot ) A[++i] ↔︎ A[j];
A[i+1] ↔︎ A[last]; // 왼쪽 부분의 마지막 한칸 옆(오른쪽 부분의 첫번째)와 피벗 교환
return i+1; // 피벗의 위치
}partition 함수의 이해를 돕기 위해 설명을 추가해 보았습니다.
- i는 피벗보다 작은 값들을 모아둔 피벗의 왼쪽 부분의 마지막을 의미합니다.
- j는 아직 재배치가 되지 않은 값들의 가장 왼쪽을 의미합니다.
- i+1에서 j-1은 피벗보다 큰 값들이 들을 모아둔 피벗의 오른쪽 부분을 의미합니다.
- 반복문이 실행될 때마다 아직 재배치되지 않은 값이 하나씩(A[j]) 피벗과 비교 후 재배치됩니다.
- j가 0부터 last-1까지 반복문이 모두 실행되고 나면 배열의 상태는 다음과 같습니다. [작은 값들][큰 값들][피벗]
- 따라서 A[i+1] ↔︎ A[last]을 수행하면 배열의 상태는 다음과 같습니다. [작은 값들][피벗][큰 값들]
- 교환 후 피벗의 위치는 i+1입니다.
저는 배열의 마지막 원소를 피벗으로 정했습니다. 피벗을 정하는 것과 피벗을 기준으로 배열을 재배치하는 것은 여러 방법으로 구현할 수 있습니다. 이에 대해서는 뒤에 구현 부분에서 다루도록 하겠습니다.
- 시간 복잡도
이 글의 처음에서 퀵 정렬의 수행시간은 평균적으로 $\Theta(n\log n)$ 이지만 최악의 경우 $\Theta(n^2)$이라고 했습니다. 퀵 정렬의 시간 복잡도를 계산해 봅시다. 입력의 크기가 n일 때 퀵 정렬의 수행시간을 $T(n)$이라고 합시다.
최선의 경우
퀵 정렬에서 최선의 경우는 피벗이 입력의 중앙값이어서 병합 정렬과 같이 배열이 항상 반반씩 균등하게 분할되는 경우입니다. 이 경우는 $T(n)$은 병합 정렬과 같은 점화식으로 나타낼 수 있습니다. 따라서 최선의 경우 소요시간은 병합 정렬과 같은 $\Theta(n\log n)$입니다.
$$T(n)=2T(\frac{n}{2})+\Theta(n)$$
여기서 $\Theta(n)$는 분할비용입니다.
최악의 경우
퀵 정렬에서 최악의 경우는 항상 배열이 한쪽으로 몰리게 분할되는 경우입니다. 입력의 마지막값 혹은 첫 번째 값을 피벗으로 사용할 때 입력이 처음부터 정렬되어 있는 경우 퀵 정렬은 한쪽으로 몰리게 분할되어 길이가 n-1과 0인 배열로 분할됩니다. 이 경우 점화식은 다음과 같이 나타낼 수 있습니다.
$$T(n)=T(n-1)+\Theta(n)$$
위 점화식을 반복 대치 혹은 마스터 정리로 계산하면 $T(n)=\Theta(n^2)$입니다. 이미 정렬되어 있는 배열을 정렬하는 것이 최악의 경우가 되는 아이러니한 상황이죠.
평균적인 경우
퀵 정렬의 수행시간은 얼마나 균형 있게 분할되는지에 달려있습니다. 평균 수행시간을 계산하는 방법은 분할 가능한 모든 경우에서의 수행시간에 대한 평균을 계산하면 됩니다. 입력의 크기 n에 대해 재배치 후 피벗의 위치를 p라 하면(위 수도코드의 p와 같습니다.) 피벗의 왼쪽 부분의 크기는 p-1, 피벗의 오른쪽 부분의 크기는 n-p입니다. 이를 점화식으로 나타내면 아래와 같습니다.
$$T(n)=T(p-1)+T(n-p)+\Theta(n)$$
가능한 모든 p에 대한 평균은 아래와 같습니다.
$$\begin{align*}T(n)&=\frac{1}{n}\displaystyle\sum_{p=1}^{n}{[T(p-1)+T(n-p)]}+n-1&\\&=\frac{2}{n}\displaystyle\sum_{k=0}^{n-1}{T(k)}+n-1&(1)\end{align*}$$
식(1)을 이용해 아래와 같이 증명하면($C(n)=T(n)$입니다.) 퀵 정렬은 평균적인 경우$\Omicron(n\log n)$의 시간이 소요됩니다.
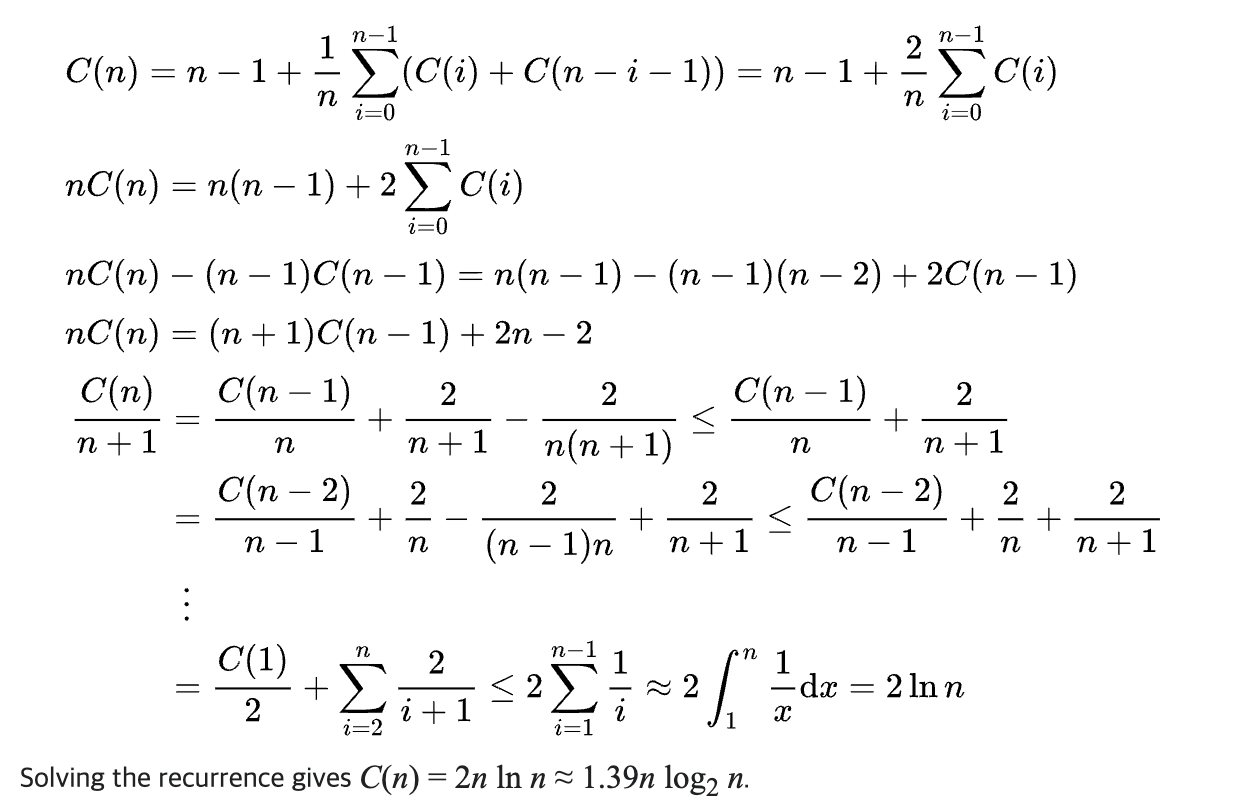
구현
- C++
int partition_start(int arr[], int start, int end) {
int p = start;
for(int i=start+1; i<=end; i++)
if(arr[i] < arr[start])
swap(arr[++p], arr[i]);
swap(arr[p], arr[start]);
return p;
}
int partition_end(int arr[], int start, int end) {
int p = start;
for(int i=start; i<end; i++)
if(arr[i] < arr[end])
swap(arr[p++], arr[i]);
swap(arr[p], arr[end]);
return p;
}
void quick_sort(int arr[], int start, int end) {
if(start < end) {
int p = partition_end(arr, start, end);
quick_sort(arr, start, p - 1);
quick_sort(arr, p + 1, end);
}
}
위에서 피벗을 정하는 방법과 피벗을 기준으로 재배치하는 방법을 더 소개해드린다고 했습니다.
# 피벗을 정하는 방법
1. Median-of-three
피벗이 입력의 중간값이면 정확히 반씩 분할되어 최선의 경우가 됩니다. 하지만 정확한 중간값을 계산하는데 정렬과 같은 시간 복잡도가 필요하겠죠. 전체 입력에 대한 중간값이 아닌 적당한 상수 k개를 뽑고 그중에서 중간값을 계산한다면 상수시간에 중간값을 계산할 수 있습니다. k개의 중간값을 피벗으로 사용한다면 최악의 경우에도 분할된 배열 중 크기가 작은 부분은 최소 $\lfloor\frac{k}{2}\rfloor$의 크기가 보장됩니다.
2. Tukey's ninther
이름에서 알 수 있듯 Tukey라는 사람이 제안했고 9개를 뽑습니다. 9개를 뽑아 3개씩 묶어 중간값 세 개를 구하고 계산된 중간값 3개의 중간값을 한번 더 구하는 방법입니다. Median of three를 트리의 형태로 두 번 사용하는 방법이죠.
3. Median of medians
Median of medians는 이름에서 알 수 있듯 중간값들의 중간값을 계산하는 방법입니다. Tukey's ninther의 일반화입니다. 입력을 상수 k개씩 그룹으로 묶으면 $\lceil\frac{n}{k}\rceil$개의 사이즈가 k이하인 그룹이 만들어집니다. 그룹에서 중간값을 계산하는 것은 위 median-of-three와 같고 상수시간이 소요됩니다. $\lceil\frac{n}{k}\rceil$개의 중간값을 구하는 것은 선형시간이 소요됩니다. 따라서 선형시간 안에 중간값들의 중간값을 계산할 수 있고 이렇게 계산된 피벗은 최악의 경우에도 일정 분할 비율을 보장합니다. 예를 들어 k가 5일 때 Median of medians로 계산된 피벗은 최악의 경우에도 7:3의 분할비율을 보장받습니다. (증명)
# 재배치 방법
1. 투포인터
투포인터를 이용해 partition 함수를 구현할 수도 있습니다. 위에서 구현한 partition함수에서 i와 j가 양쪽에서 시작해 가운데에서 교차하는 방법입니다. 아래 파이썬 구현은 투포인터로 partition 함수를 구현했습니다.
- Java
class Sort {
public static void quickSort(int[] arr, int first, int last){
if(first < last){
int p = partition(arr, first, last);
quickSort(arr, first, p-1);
quickSort(arr, p+1, last);
}
}
private static int partition(int[] arr, int first, int last){
int pivot = arr[last];
int i = first-1;
for(int j=first; j<last; j++)
if(arr[j] < pivot)
swap(arr, ++i, j);
swap(arr, i+1, last);
return i+1;
}
private static void swap(int[] arr, int i, int j){
if(i==j) return;
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}- Python
def quick_sort(arr):
def sort(first, last):
if first < last:
p = partition(first, last, pivot="first")
sort(first, p-1)
sort(p+1, last)
def partition(first, last, pivot):
method = {
"first" : first_pivot_partition,
"last" : last_pivot_partition,
}
return method[pivot](first, last)
def first_pivot_partition(first, last):
low, high, pivot = first, last, arr[first]
while low < high:
while low < high and arr[high] > pivot:
high -= 1
while low < high and arr[low] <= pivot:
low += 1
if low < high:
arr[low], arr[high] = arr[high], arr[low]
# low == high
if low is not first:
arr[low], arr[first] = arr[first], arr[low]
return low
def last_pivot_partition(first, last):
low, high, pivot = first, last, arr[last]
while low < high:
while low < high and arr[low] < pivot:
low += 1
while low < high and arr[high] >= pivot:
high -= 1
if low < high:
arr[low], arr[high] = arr[high], arr[low]
# low == high
if low is not last:
arr[low], arr[last] = arr[last], arr[low]
return low
return sort(0, len(arr) - 1)
특징
퀵 정렬은 이름에서도 알 수 있듯 평균적으로 가장 빠른 정렬 방법입니다. 최악의 경우 $\Omicron(n^2)$인데 왜 가장 빠른 걸까요? 우선 퀵 정렬은 병합 정렬과 비교해 오버헤드가 적습니다. 병합하는 과정이 필요 없고 제자리 정렬(In-place sorting)으로 메모리 관점에서도 유리합니다. 메모리 관점에서 유리하다는 것은 공간 복잡도 즉, 알고리즘을 수행하는데 필요한 메모의 크기가 작다는 의미도 있지만 지역성(Locality)이 높다는 의미도 있습니다. 지역성에는 공간적 지역성(Spacial locality)과 시간적 지역성(Temporal locality)이 있습니다.
- 공간적 지역성(Spacial locality): 방금 참조한 주소와 인접한 주소를 참조하는 특성 (예: 배열)
- 시간적 지역성(Temporal locaity): 한 번 참조한 주소를 곧 다시 참조하는 특성 (예: 반복문)
캐시 메모리는 필요한 데이터 주변 데이터 블록을 캐시에 적재 하는데 지역성이 높으면 캐시 적증률(Cache hit ratio)이 높아져 성능이 향상됩니다. 예를 들어 아래 코드에서 비슷해 보이는 A와 B 중 A가 지역성이 높고 성능이 좋습니다.
for(int i; i<n; i++){
for(int j; j<m; j++){
x = x + arr[i][j]; // A
y = y + arr[j][i]; // B
}
}매번 새로운 배열을 만드는 병합 정렬과 달리 퀵 정렬은 제자리 정렬을 하며 배열의 범위를 좁혀가며 정렬을 수행합니다. 또 위에서 살펴본 분할 기술들을 사용하면 $\Omega(n^2)$가 걸리는 최악의 경우는 피할 수 있습니다. 이러한 이유로 퀵 정렬은 구현이 쉽고 사용되는 메모리가 적으며 빨라 많은 언어에서 기본 정렬에 퀵 정렬을 사용합니다. 퀵 정렬과 병합 정렬을 비교한 글은 여기서 더 읽어보실 수 있습니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| 요세푸스 문제(Josephus problem) (0) | 2023.09.25 |
|---|---|
| [Algorithm] 병합 정렬(Merge Sort) - C++, Java, Python 구현 (0) | 2023.08.24 |
| [Algorithm] 버블 정렬(Bubble Sort) - C++, Java, Python 구현 (0) | 2023.08.22 |
| [Algorithm] 삽입 정렬(Insertion Sort) - C++, Java, Python 구현 (0) | 2023.08.22 |
| [Algorithm] 선택 정렬(Selection Sort) - C++, Java, Python 구현 (0) | 2023.08.21 |
최악의 경우 의 시간복잡도를 갖지만 평균적으로 가장 좋은 성능을 보이고 구현이 쉬워 현업에서 가장 많이 쓰인다고 알려진 퀵 정렬을 알아보고 자바와 파이썬으로 구현해 봅시다.
퀵 정렬
퀵 정렬(quick sort)은 병합 정렬 알고리즘과 비슷하게 입력을 나누어 각각에 대해 재귀적으로 정렬하는 알고리즘입니다. 퀵 정렬과 병합 정렬의 차이점은 크게 두 가지가 있습니다. 퀵 정렬은 병합 정렬과 달리 합치는 과정이 없고 입력을 항상 반씩 균등하게 나누지 않습니다. 퀵 정렬은 기준값정하고 기준값보다 큰 값들과 작은 값들로 입력을 분할합니다. 이때 기준값을 피벗(pivot)이라 합니다.
- Pseudocode
quickSort(A[], first, last){
if( first < last ){
p ← partition(A, first, last); // 피벗의 위치
quickSort(A, first, p-1);
quickSort(A, p+1, last);
}
}
partition(A[], first, last){
배열 A[first ⋯ last]의 원소들을 피벗을 기준으로 재배치하고
재배치된 피벗의 위치를 반환한다.;
}partition 함수를 조금 더 자세히 표 헌 하면 아래와 같습니다.
quickSort(A[], first, last){
if( first < last ){
p ← partition(A, first, last); // 피벗의 위치
quickSort(A, first, p-1);
quickSort(A, p+1, last);
}
}
partition(A[], first, last){
pivot ← A[last]; // 마지막 원소(A[last)를 피벗으로 사용
i ← first-1; // 피벗 왼쪽 부분의 마지막 위치 (피벗보다 작은 부분)
for( j ← first to last-1 ) // 피벗과 비교할 요소의 커서
if( A[j] < pivot ) A[++i] ↔︎ A[j];
A[i+1] ↔︎ A[last]; // 왼쪽 부분의 마지막 한칸 옆(오른쪽 부분의 첫번째)와 피벗 교환
return i+1; // 피벗의 위치
}partition 함수의 이해를 돕기 위해 설명을 추가해 보았습니다.
- i는 피벗보다 작은 값들을 모아둔 피벗의 왼쪽 부분의 마지막을 의미합니다.
- j는 아직 재배치가 되지 않은 값들의 가장 왼쪽을 의미합니다.
- i+1에서 j-1은 피벗보다 큰 값들이 들을 모아둔 피벗의 오른쪽 부분을 의미합니다.
- 반복문이 실행될 때마다 아직 재배치되지 않은 값이 하나씩(A[j]) 피벗과 비교 후 재배치됩니다.
- j가 0부터 last-1까지 반복문이 모두 실행되고 나면 배열의 상태는 다음과 같습니다. [작은 값들][큰 값들][피벗]
- 따라서 A[i+1] ↔︎ A[last]을 수행하면 배열의 상태는 다음과 같습니다. [작은 값들][피벗][큰 값들]
- 교환 후 피벗의 위치는 i+1입니다.
저는 배열의 마지막 원소를 피벗으로 정했습니다. 피벗을 정하는 것과 피벗을 기준으로 배열을 재배치하는 것은 여러 방법으로 구현할 수 있습니다. 이에 대해서는 뒤에 구현 부분에서 다루도록 하겠습니다.
- 시간 복잡도
이 글의 처음에서 퀵 정렬의 수행시간은 평균적으로 이지만 최악의 경우 이라고 했습니다. 퀵 정렬의 시간 복잡도를 계산해 봅시다. 입력의 크기가 n일 때 퀵 정렬의 수행시간을 이라고 합시다.
최선의 경우
퀵 정렬에서 최선의 경우는 피벗이 입력의 중앙값이어서 병합 정렬과 같이 배열이 항상 반반씩 균등하게 분할되는 경우입니다. 이 경우는 은 병합 정렬과 같은 점화식으로 나타낼 수 있습니다. 따라서 최선의 경우 소요시간은 병합 정렬과 같은 입니다.
여기서 는 분할비용입니다.
최악의 경우
퀵 정렬에서 최악의 경우는 항상 배열이 한쪽으로 몰리게 분할되는 경우입니다. 입력의 마지막값 혹은 첫 번째 값을 피벗으로 사용할 때 입력이 처음부터 정렬되어 있는 경우 퀵 정렬은 한쪽으로 몰리게 분할되어 길이가 n-1과 0인 배열로 분할됩니다. 이 경우 점화식은 다음과 같이 나타낼 수 있습니다.
위 점화식을 반복 대치 혹은 마스터 정리로 계산하면 입니다. 이미 정렬되어 있는 배열을 정렬하는 것이 최악의 경우가 되는 아이러니한 상황이죠.
평균적인 경우
퀵 정렬의 수행시간은 얼마나 균형 있게 분할되는지에 달려있습니다. 평균 수행시간을 계산하는 방법은 분할 가능한 모든 경우에서의 수행시간에 대한 평균을 계산하면 됩니다. 입력의 크기 n에 대해 재배치 후 피벗의 위치를 p라 하면(위 수도코드의 p와 같습니다.) 피벗의 왼쪽 부분의 크기는 p-1, 피벗의 오른쪽 부분의 크기는 n-p입니다. 이를 점화식으로 나타내면 아래와 같습니다.
가능한 모든 p에 대한 평균은 아래와 같습니다.
식(1)을 이용해 아래와 같이 증명하면(입니다.) 퀵 정렬은 평균적인 경우의 시간이 소요됩니다.
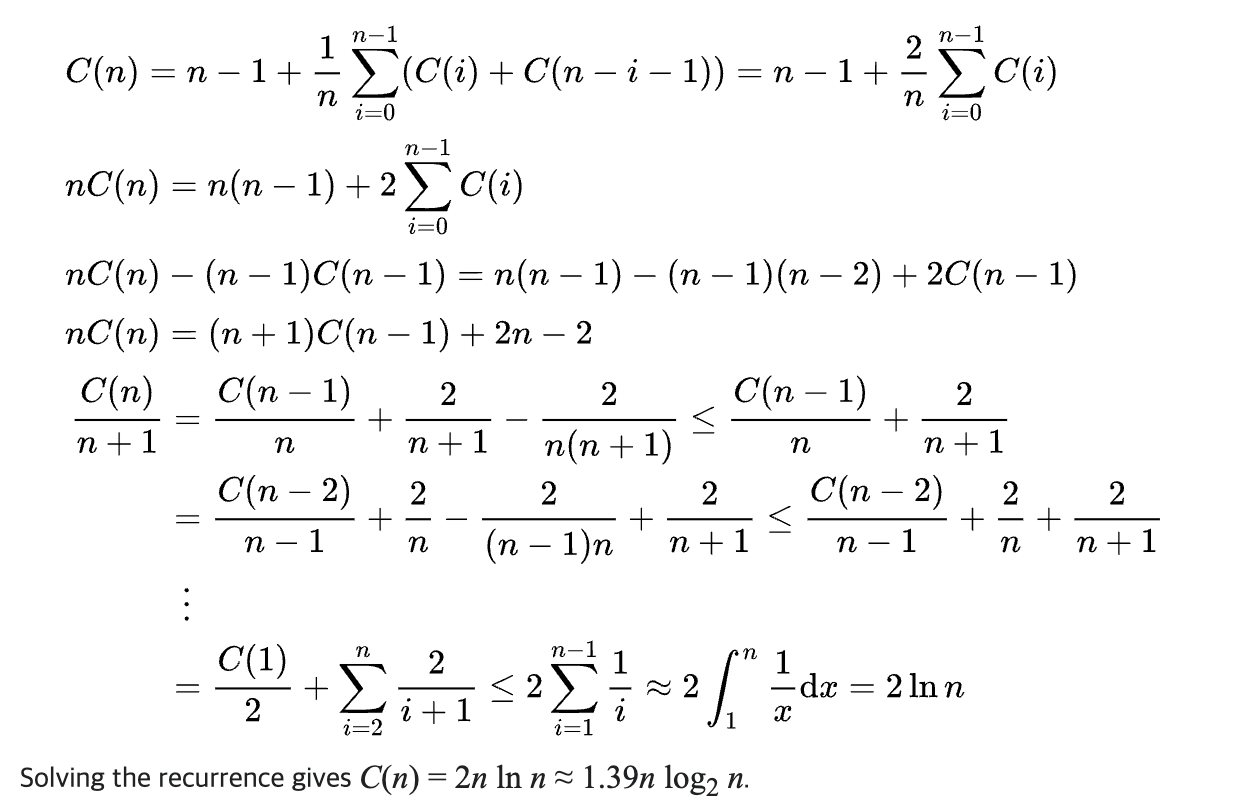
구현
- C++
int partition_start(int arr[], int start, int end) {
int p = start;
for(int i=start+1; i<=end; i++)
if(arr[i] < arr[start])
swap(arr[++p], arr[i]);
swap(arr[p], arr[start]);
return p;
}
int partition_end(int arr[], int start, int end) {
int p = start;
for(int i=start; i<end; i++)
if(arr[i] < arr[end])
swap(arr[p++], arr[i]);
swap(arr[p], arr[end]);
return p;
}
void quick_sort(int arr[], int start, int end) {
if(start < end) {
int p = partition_end(arr, start, end);
quick_sort(arr, start, p - 1);
quick_sort(arr, p + 1, end);
}
}
위에서 피벗을 정하는 방법과 피벗을 기준으로 재배치하는 방법을 더 소개해드린다고 했습니다.
# 피벗을 정하는 방법
1. Median-of-three
피벗이 입력의 중간값이면 정확히 반씩 분할되어 최선의 경우가 됩니다. 하지만 정확한 중간값을 계산하는데 정렬과 같은 시간 복잡도가 필요하겠죠. 전체 입력에 대한 중간값이 아닌 적당한 상수 k개를 뽑고 그중에서 중간값을 계산한다면 상수시간에 중간값을 계산할 수 있습니다. k개의 중간값을 피벗으로 사용한다면 최악의 경우에도 분할된 배열 중 크기가 작은 부분은 최소 의 크기가 보장됩니다.
2. Tukey's ninther
이름에서 알 수 있듯 Tukey라는 사람이 제안했고 9개를 뽑습니다. 9개를 뽑아 3개씩 묶어 중간값 세 개를 구하고 계산된 중간값 3개의 중간값을 한번 더 구하는 방법입니다. Median of three를 트리의 형태로 두 번 사용하는 방법이죠.
3. Median of medians
Median of medians는 이름에서 알 수 있듯 중간값들의 중간값을 계산하는 방법입니다. Tukey's ninther의 일반화입니다. 입력을 상수 k개씩 그룹으로 묶으면 개의 사이즈가 k이하인 그룹이 만들어집니다. 그룹에서 중간값을 계산하는 것은 위 median-of-three와 같고 상수시간이 소요됩니다. 개의 중간값을 구하는 것은 선형시간이 소요됩니다. 따라서 선형시간 안에 중간값들의 중간값을 계산할 수 있고 이렇게 계산된 피벗은 최악의 경우에도 일정 분할 비율을 보장합니다. 예를 들어 k가 5일 때 Median of medians로 계산된 피벗은 최악의 경우에도 7:3의 분할비율을 보장받습니다. (증명)
# 재배치 방법
1. 투포인터
투포인터를 이용해 partition 함수를 구현할 수도 있습니다. 위에서 구현한 partition함수에서 i와 j가 양쪽에서 시작해 가운데에서 교차하는 방법입니다. 아래 파이썬 구현은 투포인터로 partition 함수를 구현했습니다.
- Java
class Sort {
public static void quickSort(int[] arr, int first, int last){
if(first < last){
int p = partition(arr, first, last);
quickSort(arr, first, p-1);
quickSort(arr, p+1, last);
}
}
private static int partition(int[] arr, int first, int last){
int pivot = arr[last];
int i = first-1;
for(int j=first; j<last; j++)
if(arr[j] < pivot)
swap(arr, ++i, j);
swap(arr, i+1, last);
return i+1;
}
private static void swap(int[] arr, int i, int j){
if(i==j) return;
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
}- Python
def quick_sort(arr):
def sort(first, last):
if first < last:
p = partition(first, last, pivot="first")
sort(first, p-1)
sort(p+1, last)
def partition(first, last, pivot):
method = {
"first" : first_pivot_partition,
"last" : last_pivot_partition,
}
return method[pivot](first, last)
def first_pivot_partition(first, last):
low, high, pivot = first, last, arr[first]
while low < high:
while low < high and arr[high] > pivot:
high -= 1
while low < high and arr[low] <= pivot:
low += 1
if low < high:
arr[low], arr[high] = arr[high], arr[low]
# low == high
if low is not first:
arr[low], arr[first] = arr[first], arr[low]
return low
def last_pivot_partition(first, last):
low, high, pivot = first, last, arr[last]
while low < high:
while low < high and arr[low] < pivot:
low += 1
while low < high and arr[high] >= pivot:
high -= 1
if low < high:
arr[low], arr[high] = arr[high], arr[low]
# low == high
if low is not last:
arr[low], arr[last] = arr[last], arr[low]
return low
return sort(0, len(arr) - 1)
특징
퀵 정렬은 이름에서도 알 수 있듯 평균적으로 가장 빠른 정렬 방법입니다. 최악의 경우 인데 왜 가장 빠른 걸까요? 우선 퀵 정렬은 병합 정렬과 비교해 오버헤드가 적습니다. 병합하는 과정이 필요 없고 제자리 정렬(In-place sorting)으로 메모리 관점에서도 유리합니다. 메모리 관점에서 유리하다는 것은 공간 복잡도 즉, 알고리즘을 수행하는데 필요한 메모의 크기가 작다는 의미도 있지만 지역성(Locality)이 높다는 의미도 있습니다. 지역성에는 공간적 지역성(Spacial locality)과 시간적 지역성(Temporal locality)이 있습니다.
- 공간적 지역성(Spacial locality): 방금 참조한 주소와 인접한 주소를 참조하는 특성 (예: 배열)
- 시간적 지역성(Temporal locaity): 한 번 참조한 주소를 곧 다시 참조하는 특성 (예: 반복문)
캐시 메모리는 필요한 데이터 주변 데이터 블록을 캐시에 적재 하는데 지역성이 높으면 캐시 적증률(Cache hit ratio)이 높아져 성능이 향상됩니다. 예를 들어 아래 코드에서 비슷해 보이는 A와 B 중 A가 지역성이 높고 성능이 좋습니다.
for(int i; i<n; i++){
for(int j; j<m; j++){
x = x + arr[i][j]; // A
y = y + arr[j][i]; // B
}
}매번 새로운 배열을 만드는 병합 정렬과 달리 퀵 정렬은 제자리 정렬을 하며 배열의 범위를 좁혀가며 정렬을 수행합니다. 또 위에서 살펴본 분할 기술들을 사용하면 가 걸리는 최악의 경우는 피할 수 있습니다. 이러한 이유로 퀵 정렬은 구현이 쉽고 사용되는 메모리가 적으며 빨라 많은 언어에서 기본 정렬에 퀵 정렬을 사용합니다. 퀵 정렬과 병합 정렬을 비교한 글은 여기서 더 읽어보실 수 있습니다.
'Computer Science > Algorithm' 카테고리의 다른 글
| 요세푸스 문제(Josephus problem) (0) | 2023.09.25 |
|---|---|
| [Algorithm] 병합 정렬(Merge Sort) - C++, Java, Python 구현 (0) | 2023.08.24 |
| [Algorithm] 버블 정렬(Bubble Sort) - C++, Java, Python 구현 (0) | 2023.08.22 |
| [Algorithm] 삽입 정렬(Insertion Sort) - C++, Java, Python 구현 (0) | 2023.08.22 |
| [Algorithm] 선택 정렬(Selection Sort) - C++, Java, Python 구현 (0) | 2023.08.21 |
