연결 리스트의 가장 기본이 되는 단일 연결 리스트로 연결 리스트를 이해해 봅시다.
연결 리스트
`연결 리스트(linked list)`는 데이터와 다음 데이터의 위치를 함께 저장하여 데이터들을 체인처럼 연결하는 자료 구조입니다. 여기서 저장되는 자료의 단위(데이터와 다음 자료의 위치를 묶은 구조체)를 `노드(node)`라고 부릅니다. 다시 말하면 연결 리스트는 데이터와 다음 노드의 참조값을 갖는 노드들로 연결된 자료 구조입니다. 연결 리스트는 연결되는 방법에 따라 `단일 연결 리스트(singly linked list)`, `이중 연결 리스트(doubly linked list)`, `다중 연결 리스트(multi-linked list)`, `원형 연결 리스트(circular linked list)`등으로 구분됩니다. 이번 글에서는 가장 기본이 되는 단일 연결 리스트에 대해 알아보겠습니다. 기본 개념만 안다면 다른 연결 리스트도 이해하실 수 있으실 겁니다.
단일 연결 리스트
`단일 연결 리스트(singly linked list)`는 노드와 노드 사이를 연결하는 참조값이 하나인 연결 리스트입니다. 데이터를 저장한 노드가 다음 노드의 참조값을 가지고 있어 노드를 체인 형태로 연결한 자료 구조입니다.
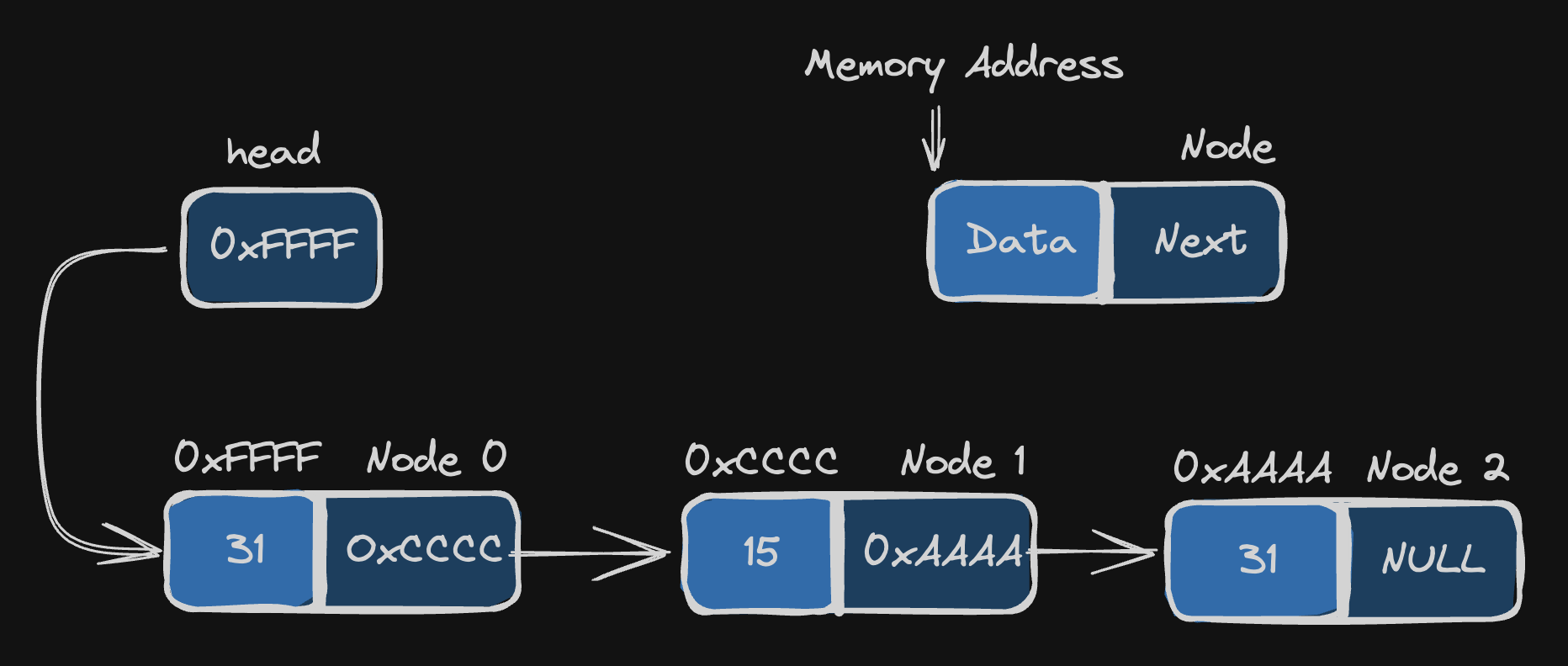
위 그림은 단일 연결 리스트를 간단하게 표현한 그림입니다. 노드에는 값과 다음 노드의 주소가 저장되며 저장된 주소를 타고 모든 노드를 탐색할 수 있습니다. 그렇다 보니 2번 노드에 가기 위해서는 1번 노드를 거쳐야 하고 1번 노드에 가기 위해서는 0번 노드를 거쳐합니다. 즉 단방향 `순차접근(sequential access)`만 가능합니다.(이중 연결 리스트에서는 양방향으로 가능합니다.)
- 장점
연결 리스트는 1차원 자료구조라는 점에서 배열과 자주 비교됩니다. 저장공간의 크기를 미리 설정해야 하는 배열과 다르게 연결 리스트는메모리만 있다면 무한하게 확장이 가능합니다. 또 데이터의 삽입/삭제 시 해당 데이터의 뒷부분을 모두 복사해야 하는 배열과 달리 참조값의 변경만으로 보다 적은 연산으로 삽입/삭제가 가능합니다.
- 자료의 삽입/삭제에 드는 비용이 적다.
- 확장/축소에 용이하다.
- 메모리상에서 데이터의 이동이 필요 없다.
- 단점
하지만 위에서 언급했든 순차접근만 가능하므로 `무작위 접근(random access)`이 가능한 배열에 비해 읽기 성능이 현저히 떨어집니다. 여기에 한술 더 떠 연속된 메모리에 저장하는 배열에 비해 메모리 어딘가에 저장 후 메모리 주소로 연결된 연결 리스트는 `지역성(locality)`이 떨어져 순차접근마저도 배열에 비해 성능이 안 좋습니다. 또 데이터 이외에도 주소를 저장할 메모리가 추가로 소모됩니다.
- 순차 접근으로 인한 낮은 읽기 성능
- 연속된 메모리에 저장되지 않는 낮은 지역성
- 메모리 주소 저장에 의한 메모리 오버헤드
- 시간 복잡도
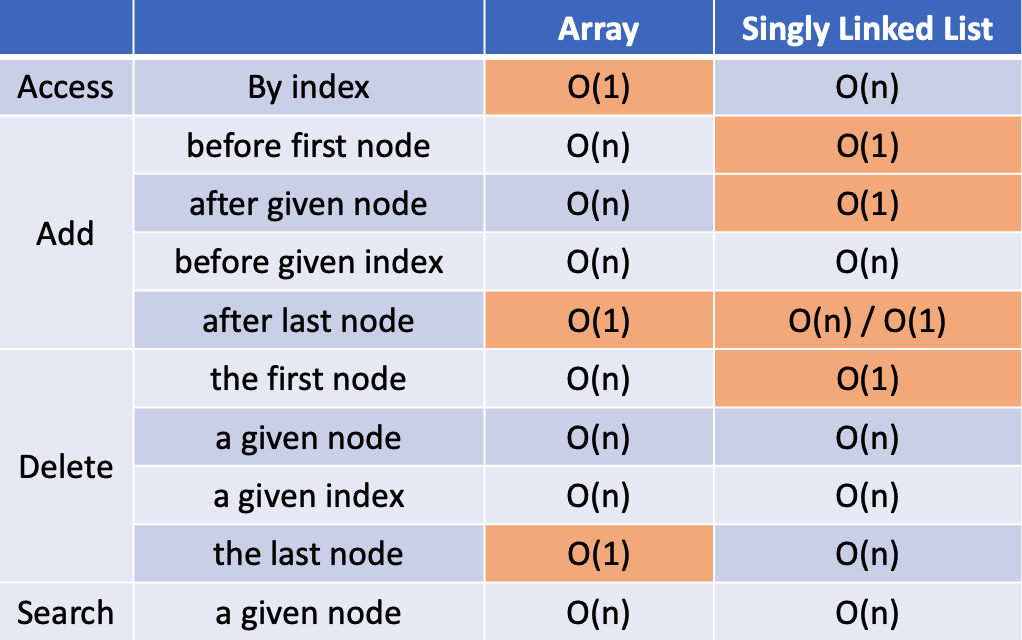
단일 연결 리스트의 마지막에 추가하는 것은 마지막 노드의 주소를 기억하는 방법으로 상수시간으로 줄일 수 있습니다. 하지만 마지막 요소 삭제는 선형 시간이 소요됩니다. 삭제는 직전 요소를 알아야하지만 마지막 요소에서 직전요소를 알 수 없어 결국 첫 요소부터 탐색해야 하기 때문입니다. 따라서 추가/삭제가 잦고 전체 양을 모르거나 변동이 심한 데이터의 경우 연결 리스트를 사용하는 것이 좋습니다.
Java 구현
- 구현 시 주의할 점
1. 삽입/삭제 순서
그림으로 보면 연결 리스트가 어떻게 데이터를 저장하는지 직관적으로 이해하기 쉽습니다. 연결리스트의 추가, 제거에는 주의할 점이 있습니다. 데이터를 추가하는 상황으로 설명드리겠습니다. 추가하는 위치에 따라 크게 세 가지 경우로 나눌 수 있고 각각의 경우에서 연결 리스트의 크기를 고려해 주어야 합니다.
- 가장 앞에 추가(크기가 0인 경우, 1 이상인 경우)
- 중간에 추가(크기가 2 이상인 경우)
- 가장 뒤에 추가(크기가 0인 경우, 1 이상인 경우)


가장 뒤에 추가하는 경우는 새로운 노드를 마지막 노드에 연결하면 되지만 앞과 중간에 추가할 때는 주의할 점이 있습니다. 새로운 노드를 연결할 때 순서를 지켜줘야 합니다. 순서가 중요한 이유는 만약 그림과 달리 순서를 2 → 1의 순서로 진행하게 되면 2를 진행한 후 node0를 참조하는 변수가 없어져 node0을 newNode에 붙일 수 없고 node0과 node0에 달린 노드들은 가비지 컬랙팅 대상이 됩니다. 조립은 분해의 역순! 삭제는 추가의 반대로 진행하면 됩니다.
2. Size, Tail
단일 연결 리스트는 단방향 순차 접근만 가능합니다. 따라서 마지막 노드까지 가기 위해서는 모든 노드를 거쳐야합니다. 크기를 구하거나 연결 리스트의 끝에 새로운 요소를 추가 할 때 θ(n)의 시간 복잡도가 소요됩니다. 이는 전체 크기를 저장하는 size 필드와 마지막 노드의 주소를 저장하는 tail 필드를 추가해 상수시간으로 성능을 향상할 수 있습니다.
- 단일 연결 리스트 구현
이번 글에서는 단일 연결 리스트의 CRUD(추가, 검색, 수정, 삭제)를 Java로 구현합니다.
이중 연결 리스트의 구현은 Deque를 구현하는 글에서 확인 하실 수 있습니다. Java에서 제공하는 이중 연결 리스트의 코드는 이곳에서 확인할 수 있습니다.
import java.util.StringJoiner;
import java.util.Iterator;
import java.util.NoSuchElementException;
class SinglyLinkedList<E> implements Iterable<E> {
class Node<E> {
E data;
Node<E> next = null;
Node(E element) { data = element; }
}
private Node<E> head = null, tail = null;
private int size = 0;
// private 메서드
private Node<E> node(int index) {
Node<E> x = head;
for(int i = 0; i < index; i++)
x = x.next;
return x;
}
private boolean isDataIndex(int index) {
return index >=0 && index < size;
}
// 기본 메서드
public int size() { return size; }
public void clear() { head = tail = null; size = 0; }
public boolean isEmpty() { return head == null; }
// 추가(addFirst, addLast, insert)
public boolean addFirst(E element) {
final Node<E> newNode = new Node<>(element);
if(isEmpty())
tail = newNode;
else
newNode.next = head;
head = newNode;
size++;
return true;
}
public boolean addLast(E element) {
final Node<E> newNode = new Node<>(element);
if(isEmpty())
head = newNode;
else
tail.next = newNode;
tail = newNode;
size++;
return true;
}
public boolean insert(int index, E element) {
if(index == 0)
return addFirst(element);
if(index == size)
return addLast(element);
if(!isDataIndex(index))
return false;
final Node<E> newNode = new Node<>(element);
final Node<E> prev = node(index - 1);
newNode.next = prev.next;
prev.next = newNode;
size++;
return true;
}
// 검색(getFirst, getLast, get)
public E getFirst() {
return isEmpty() ? null : head.data;
}
public E getLast() {
return isEmpty() ? null : tail.data;
}
public E get(int index) {
if(!isDataIndex(index))
return null;
return node(index).data;
}
// 수정(set)
public E set(int index, E element) {
if(!isDataIndex(index))
return null;
final Node<E> x = node(index);
final E oldValue = x.data;
x.data = element;
return oldValue;
}
// 삭제(remove)
public E removeFirst() {
if(isEmpty())
return null;
final Node<E> h = head;
final E element = h.data;
final Node<E> next = h.next;
h.data = null;
h.next = null; // help gc
if(next == null)
tail = null;
head = next;
size--;
return element;
}
public E removeLast() {
if(head == tail) // size < 2
return removeFirst();
final Node<E> prev = node(size-2);
final E element = tail.data;
tail.data = null; // help gc
prev.next = null;
tail = prev;
size--;
return element;
}
public E removeAt(int index) {
if(!isDataIndex(index))
return null;
if(index == 0)
return removeFirst();
if(index == size-1)
return removeLast();
final Node<E> prev = node(index-1);
final Node<E> x = prev.next;
final E element = x.data;
prev.next = x.next;
x.data = null;
x.next = null; // help gc
size--;
return element;
}
public boolean remove(Object obj) {
// size == 0
if(isEmpty())
return false;
// size == 1
if(head == tail) {
if(obj == null && head.data == null ||
obj != null && obj.equals(head.data)) {
removeFirst();
return true;
}
return false;
}
// size > 1
if(obj == null) {
if(head.data == null) {
removeFirst();
return true;
}
for(Node<E> prev = head; prev.next != null; prev = prev.next) {
if(prev.next.data == null) {
Node<E> x = prev.next;
prev.next = x.next;
if(x.next == null)
tail = prev;
else
x.next = null; // help gc
return true;
}
}
} else {
if(obj.equals(head.data)){
removeFirst();
return true;
}
for(Node<E> prev = head; prev.next != null; prev = prev.next) {
if(obj.equals(prev.next.data)) {
Node<E> x = prev.next;
prev.next = x.next;
if(x.next == null)
tail = prev;
else
x.next = null; // help gc
x.data = null; // help gc
return true;
}
}
}
return false;
}
// 추가 메서드
public boolean contains(E obj) {
Node<E> x = head;
while(x != null) {
if(obj == null && x.data == null ||
obj != null && obj.equals(x.data)) {
return true;
}
x = x.next;
}
return false;
}
@Override
public String toString() {
Node<E> x = head;
StringJoiner joiner = new StringJoiner(",","[","]");
while(x != null) {
joiner.add(x.data.toString());
x = x.next;
}
return joiner.toString();
}
class IteratorHelper implements Iterator<E> {
Node<E> x = head;
public boolean hasNext(){
return x != null;
}
public E next() {
if(!hasNext())
throw new NoSuchElementException();
E value = x.data;
x = x.next;
return value;
}
}
@Override
public Iterator<E> iterator() {
return new IteratorHelper();
}
}
'Computer Science > Data Structure' 카테고리의 다른 글
| Table of Contents - 자료구조, 알고리즘 (0) | 2023.09.04 |
|---|---|
| [자료 구조] 큐(Queue) - 단일 연결 리스트를 이용한 Deque, Java 구현 (2) | 2023.09.04 |
| [자료 구조] 스택(Stack) - 단일 연결 리스트와 배열을 이용한 스택, Java 구현 (0) | 2023.09.01 |
